Non-optimization Problem Which Approach Is Used Branch and Bound
This is particularly helpful when the number of copying subproblems is exponentially large. In Branch Bound algorithm a given subproblem which cannot be bounded has to be divided into at least two new restricted subproblems.

A Flow Chart Of Hybrid Algorithm In Which Branch And Bound Method Is Download Scientific Diagram
Used for solving discrete quadratic optimization problems in particular in the binary case.

. Abstract A new branch-and-bound based algorithm for smooth nonconvex multiobjective optimization problems with convex constraints is presented. 4 Depth First Branch and Bound MultiObjective Branch-and-Bound MO-BB is a recursive description of a generic search schema for MO-WCSP solving. Partition feasible set into convex sets and find lowerupper bounds for each.
You should have a routine to find upper bound of optimal min value. While most work has been focused on developing problem-specific techniques little is known about how to systematically design the node searching strategy on a branch-and-bound tree. You can do it eg.
Branch and bound is an algorithm design paradigm for discrete and combinatorial optimization problems as well as mathematical optimization. During search MO-BB maintains a set of non- dominated p-vectors corresponding to the best solutions found so far. To determine a good approximated Pareto front for this type of problems we propose a general hybrid approach based on a Multi Criteria Branch-and.
Branch and bound algorithms are used to find the optimal solution for combinatory discrete and general mathematical optimization problems. Basic idea of branch and bound - partition domain into convex sets and improve lowerupper bound in your case it is intervals. Since the solution is a permutation of the n jobs its complexity is O n.
Branch-and-bound is a widely used method in combinatorial optimization in-cluding mixed integer programming structured prediction and MAP inference. For each child wof v If wcannot lead to a solution then prune ie. An algorithm design technique primarily for solving hard optimization problems.
Bound on the optimal value over a given region upper bound can be found by choosing any point in the region or by a local optimization method lower bound can be found from convex relaxation duality Lipschitz or other bounds. Branch and bound is an algorithm design paradigm which is generally used for solving combinatorial optimization problems. Up to 10 cash back This paper presents a new branchbound approach for solving nonlinear fractional multi-objective optimization problem.
Do not add wto the PromisingSet. It therefore needs less storage and less time than Branch and Bound. The algorithm computes an.
Branch and Bound solve these problems relatively quickly. These problems typically exponential in terms of time complexity and may require exploring all possible permutations in worst case. A branch-and-bound algorithm consists of a systematic enumeration of candidate solutions by means of state space search.
When a solution is found it will be good but it may be less than optimal. Although branch-and-bound is often dis- cussed in the context of integer program- ming it is actually a general approach that can also be applied to solve many combi- natorial optimization. Best-First Search is a blind variant of Branch and Bound in which future costs are all assumed to be equal.
Does not necessarily guarantee worst case polynomial time complexity. We provide a provably optimal algorithm and demonstrate good performance on both synthetic and real data. Using the weak duality theorem of Lagrange of nonlinear programming and vertices of simplicial during the branchbound search lower and upper bounds are computed.
In general given an NP-Hard problem a branch and bound algorithm explores the entire search space of possible solutions and provides an optimal solution. Guarantees that the optimal solution will be found. The optimization scheme is based on ideas from global optimization theory in particular convex underestimators in combination with branch-and-bound methods.
It searches depth-first the tree defined by the problem. When a solution is found it is the cheapest but for reasons recently discussed such a search is rarely practical. Branch-and-bound is a widely used method in combinatorial optimization in-cluding mixed integer programming structured prediction and MAP inference.
For solving the resulting SDPs Q-MIST uses an off-the-shelf interior point algorithm. 1 Introduction Many problems in engineering physics economics and other subjects may be reduced to problems of global minimization. We also give examples of where traditional methods fail due to the local minima problem.
The set of candidate solutions is thought of as forming a rooted tree with the full set at the root. For the general non-convex integer case with box constraints the branch-and-bound algorithm Q-MIST has been proposed by Buchheim and Wiegele Math Program. While most work has been focused on developing problem-specific techniques little is known about how to systematically design the node searching strategy on a branch-and-bound tree.
Branch-and-Bound PromisingSet root currentbestvalueor based on problem type While PromisingSet6Do Pick a promising member vof the PromisingSet If vis a solution then update currentbest valuesolution Otherwise expand v. Global optimization branch and bound simplicial partitions. -approximation of all globally optimal solutions.
For the general non-convex integer case with box constraints the branch-and-bound algorithm Q-MIST has been proposed 11 which is based on an extension of the well-known SDP-relaxation for max-cut. To describe the process to obtain equivalent fuzzy MOLF optimization problem consider a non-convex optimization problem and we can take n i x 0 for all x Q and the problem becomes as 2 Z ˆ x min n 1 x d 1 x n 2 x d 2 x n p x d p x subject to x Q x R n A x b A R l n b R l x 0 In problem d i x is convex function on R n. Mathematically the problem of global optimization is formulated as f min xD fx.
Dynamic Programming is frequently related to Optimization Problems. We introduce the algorithm which uses selection rules discarding and termination tests. Up to 10 cash back Semidefinite programming SDP relaxations have been intensively used for solving discrete quadratic optimization problems in particular in the binary case.
Branch and Bound algorithm are methods for global. The Hungarian algorithm has worst case run-time complexity of O. The optimal assignment can be found using the Hungarian algorithm.
Just by sampling subdomain and take smallest or use local optimization method start from random point.

7 Branch And Bound Introduction Youtube

A Sketch Of The Working Principle Of The Branch And Bound Method For A Download Scientific Diagram
![]()
Branch Bound Algorithms Ppt Video Online Download

0 1 Knapsack Using Branch And Bound Geeksforgeeks

Pdf Branch And Bound Algorithms
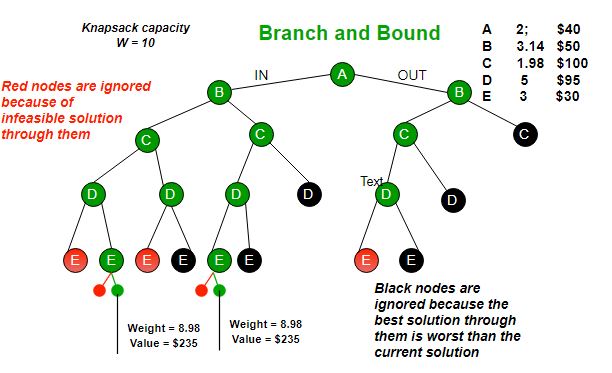
Branch And Bound Algorithm Geeksforgeeks

Implementation Of 0 1 Knapsack Using Branch And Bound Geeksforgeeks

Branch And Bound Technique For Integer Programming Youtube

Branch And Bound Bb Optimization

Pdf Branch And Bound Algorithms

Pdf Branch And Bound Algorithms Principles And Examples Semantic Scholar

Branch And Bound Bb Optimization
Type Of Solutions For Optimization Problems Download Scientific Diagram

Traveling Salesman Problem Using Branch And Bound Geeksforgeeks

Flowchart Of The Branch And Price Method Download Scientific Diagram

2 Illustration Of The Sequential Branch And Bound Algorithm Download Scientific Diagram

Comments
Post a Comment